On the limits of 90° static light scattering for determining weight average molar mass Mw
A discussion with Chief Science Officer, Dr. Wayne Reed
This Technical Note assesses the fractional error in Mw that results when θ=90° static light scattering detection is used, instead of a full angular extrapolation via MALS.
Question: Can you compare the differences in determining Mw with multi-angle light scattering (MALS) and static light scattering (SLS)?
Answer: Determination of Mw by static light scattering can typically be made using multi-angle light scattering (MALS) for polymers and colloids in the nanoscale range. Most modern MALS uses vertically polarized incident light, and detection takes place in the plane perpendicular to the vertical electric polarization plane, the so-called ‘scattering plane.’ When the characteristic dimension of a scatterer is much less than the incident wavelength λ, the particle is termed a ‘Rayleigh scatterer,’ whose scattering intensity is equal at all angles in the scattering plane.
In such cases it is sufficient to determine the scattering intensity at a single angle to determine Mw. A good example of where static light scattering is adequate is a native monoclonal antibody, whose size (~10 nm)<<λ. When the characteristic dimension is a significant fraction of λ, then it is necessary to measure scattering intensity at various angles and extrapolate to zero angle, θ=0, in order to determine Mw.
Question: Can you review Raleigh scattering?
Answer: There are several levels of approximation in approaching the analysis of light scattering data. The simplest is the Rayleigh approximation where there is no significant angular dependence of the scattering. Next, the so-called Rayleigh-Debye approximation is often used. This approximation assumes that the angular dependence of scattering is due to phase differences at the detection angle θ caused only by the geometrical path length differences among scattering elements in a scattering body.
This is usually an excellent approximation for polymers since the scatterers resemble threads immersed in a solvent. The Rayleigh-Debye range is more restricted for solid colloids, since the phase shift at the detector between scattering elements is due both to their geometrical path difference and the contrast of index of refraction between the solid object and the solvent.
Question: How does this relate to the Zimm equation and virial coefficients?
Answer: The Zimm equation for dilute polymer solutions that results in the Rayleigh-Debye approximation is
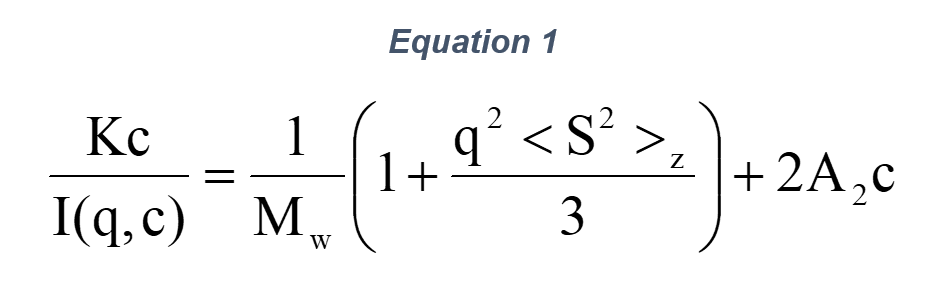
where I(q,c) is the excess Rayleigh scattering ratio (in units of cm-¹), the quantity measured by the light scattering instrument, equal to its value from the polymer solution minus the value from the pure solvent.
In equation 1, q is the usual scattering wave-vector amplitude, q=(4πn/λo)sin(θ/2), where n is the solvent index of refraction, λo is the vacuum wavelength of the incident light, dn/dc is the differential refractive index for the polymer in the chosen solvent, and A2 is the second virial coefficient (also often represented as B22), and <S²>z is the mean square radius of gyration. K is an optical constant, given for vertically polarized incident light by
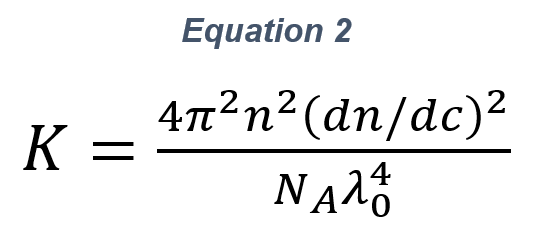
The term involving A2 can be considered if the value of A2 is known, or it can be ignored if 2A2cMw<<1.
Question: How does this relate back to the error when determining Mw? Furthermore, how does this relate to an instrument using a single angle at 90° like ARGEN?
Answer: Within this paradigm, the error in Mw can be readily assessed. I(0,c) is the Rayleigh ratio extrapolated to θ=0, whereas I(q≠0,c) is the value measured at any θ>0. If this latter value is used, then an apparent Mw is computed, termed Mw’, which is smaller than the true Mw. Equation 1 (either accounting for A2 or ignoring it) gives the ratio of Mw’ to Mw as
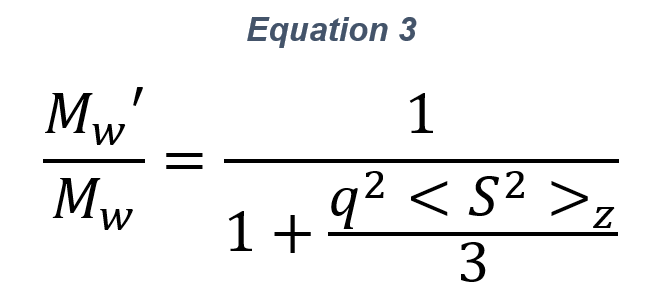
Using values appropriate for ARGEN applied to aqueous solutions, λ0=660 nm, n=1.33, θ=90°, then equation 3 becomes
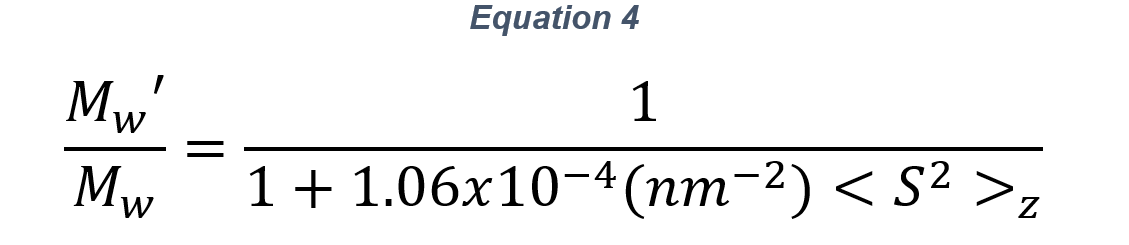
Question: How do these equations relate to product development? For example, a monoclonal antibody (mAb)?
Answer: First, consider the error in Mw for a native mAb with a typical hydrodynamic diameter DH=10 nm. The relationship between a spheroidal object’s DH and <S2>1/2 is
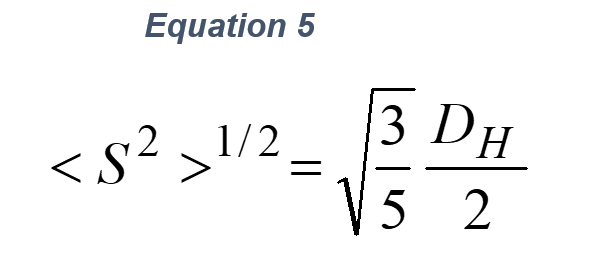
The substitution of <S2>1/2=3.87 nm into equation 5 shows the error in Mw for a typical native mAb is only 0.16% using ARGEN.
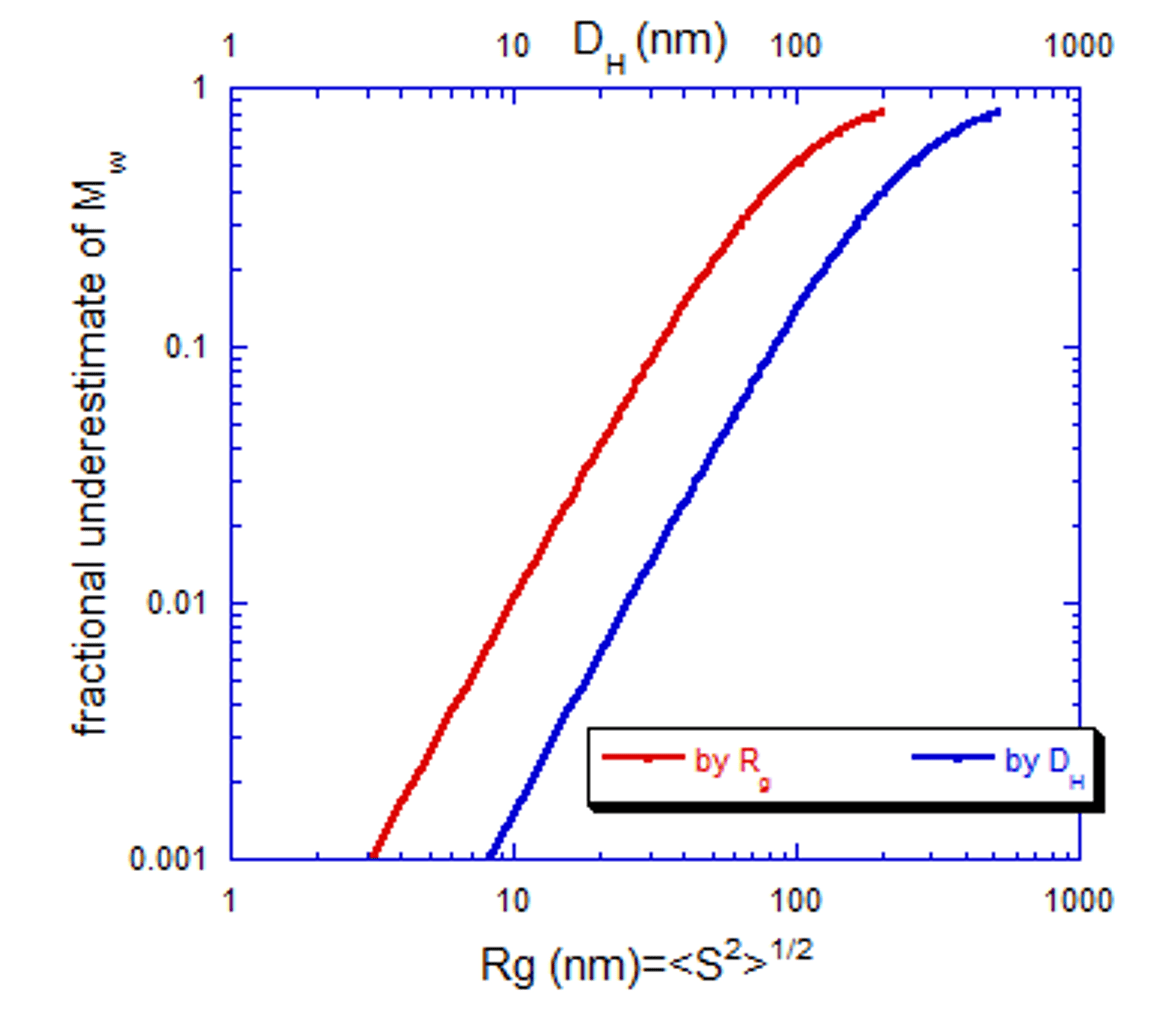
Figure 1 shows the fractional underestimate error of Mw vs both Rg=<S2>1/2 and for equivalent spheroidal DH.
It is important to note that full angular extrapolations of MALS under the Zimm approximation will also fail as the characteristic dimension of the scatterers approaches λ.
Question: What’s your conclusion on the limits of 90° static light scattering for the determination of weight-average molar mass Mw?
Answer: Using ARGEN’s θ=90° detection, globular proteins of this density (like mAbs) could be measured up to 304 M0 or 4.16×107 g/mol with only 10% error.


